核范数优化简介

版权声明:图片来源网络,仅做分享之用!侵权请联系删除。
核范数优化是一种在机器学习和数据分析中常用的方法,它通过使用核函数来处理高维数据,从而避免了传统机器学习算法在处理高维数据时遇到的困难,核范数优化也称为核优化,旨在寻找一种基于核函数的最优化算法,以达到更高的性能和精度。
核范数优化的基本思想是在使用传统的最小二乘法或其他线性优化方法之前,首先通过核函数将数据转化为低维空间,然后在低维空间上执行优化算法,这种方法的优点在于它能够有效地处理高维数据,并且能够避免传统机器学习算法在处理高维数据时遇到的维度灾难问题。
核范数优化算法通常包括以下几个步骤:使用核函数将高维数据转化为低维空间;在低维空间上执行传统的优化算法,如梯度下降、牛顿法等;根据优化结果对数据进行分类或回归分析,核范数优化算法具有较高的效率和准确性,因此被广泛应用于各种机器学习和数据分析任务中。
核范数优化是一种有效的机器学习和数据分析方法,它通过使用核函数将高维数据转化为低维空间,并在低维空间上执行优化算法,以达到更高的性能和精度,随着人工智能技术的不断发展,核范数优化将在未来的机器学习和数据分析领域发挥越来越重要的作用。
核范数优化:原理、应用与发展趋势
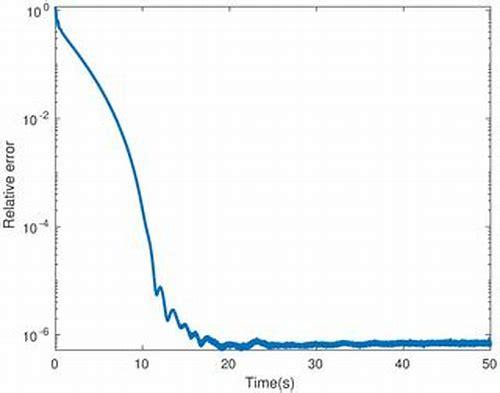
版权声明:图片来源网络,仅做分享之用!侵权请联系删除。
在当今数据驱动的时代,核范数优化作为一种特殊的数学优化方法,正逐渐在多个领域崭露头角,成为解决复杂问题的有效工具,它不仅在理论上具有深厚的内涵,更在实际应用中展现出强大的潜力,为众多学科和行业带来了新的突破与变革。
一、核范数优化的原理剖析
核范数,也称为矩阵的迹范数,是矩阵的一种特殊范数形式,对于一个矩阵 \(A\),其核范数定义为 \(||A||_= \sum_{i=1}^n \sigma_i(A)\),\(\sigma_i(A)\) 表示矩阵 \(A\) 的第 \(i\) 个奇异值,核范数优化的核心思想是通过最小化或约束矩阵的核范数,来实现对矩阵结构特征的提取和优化。
从数学角度来看,核范数优化问题通常可以表示为
\[
\min_{X} ||X||_\quad \text{s.t.} \quad A(X) = b
\]
\(X\) 是待优化的矩阵变量,\(A(\cdot)\) 是线性映射,\(b\) 是给定的观测向量或矩阵,这个问题的本质是在满足一定约束条件下,寻找核范数最小的矩阵 \(X\),这种优化问题往往具有凸优化的特性,即存在全局最优解,这使得核范数优化在理论上具有良好的可处理性。
在图像恢复领域,假设我们有一个受损的图像,其像素矩阵可以表示为 \(X\),由于图像在传输或存储过程中受到了噪声干扰或部分数据丢失,我们需要通过核范数优化来恢复原始图像,具体来说,我们可以利用图像的先验信息,如图像的稀疏性或低秩性,构建一个关于 \(X\) 的核范数优化问题,通过求解这个问题,我们可以得到一个核范数最小的矩阵 \(X\),这个矩阵在一定程度上能够逼近原始图像,从而实现图像的恢复。
二、核范数优化的应用领域
(一)机器学习与数据分析
在机器学习中,核范数优化被广泛应用于特征选择、维度约简和分类等问题,在主成分分析(PCA)中,通过最小化数据的协方差矩阵的核范数,可以找到数据的主要特征方向,从而实现数据的降维,这不仅可以减少数据的存储和计算成本,还可以提高模型的泛化能力。
在监督学习中,核范数优化可以用于构建稀疏编码模型,通过将样本的特征表示为字典矩阵的稀疏线性组合,并约束字典矩阵的核范数,可以实现特征的自动选择和编码,这种方法在文本分类、图像识别等领域取得了良好的效果。
(二)信号处理与压缩感知
信号处理是核范数优化的另一个重要应用领域,在压缩感知中,通过利用信号的稀疏性,可以将高维信号压缩为低维观测值,并在接收端通过核范数优化算法恢复原始信号,这种方法在无线通信、图像压缩等方面具有广泛的应用前景。
在无线通信中,由于信道带宽的限制,我们需要对传输的信号进行压缩,通过采用压缩感知技术,可以在发送端对信号进行稀疏表示,并只传输少量的观测值,在接收端,利用核范数优化算法可以根据这些观测值恢复出原始信号,从而大大提高了通信的效率和可靠性。
(三)计算机视觉
计算机视觉中的许多任务,如图像去噪、图像填充、视频背景建模等,都可以转化为核范数优化问题,以图像去噪为例,假设我们有一幅含噪图像 \(Y = X + N\),\(X\) 是原始图像,\(N\) 是噪声,我们可以将图像去噪问题建模为一个核范数优化问题
\[
\min_{X} ||Y - X||_F^2 + \lambda ||X||_*
\]
\(||\cdot||_F\) 表示矩阵的 Frobenius 范数,\(\lambda\) 是正则化参数,通过求解这个问题,我们可以得到一个去噪后的图像 \(X\),它在去除噪声的尽可能地保留了图像的细节和结构信息。
三、核范数优化的算法与挑战
(一)常用算法
求解核范数优化问题的常用算法包括交替方向乘子法(ADMM)、增广拉格朗日乘子法(ALM)和奇异值阈值算法(SVT)等。
ADMM 是一种高效的分布式优化算法,它将原问题分解为多个子问题,并通过交替迭代的方式求解,在核范数优化中,ADMM 可以将问题分解为关于矩阵 \(X\) 和辅助变量 \(Z\) 的两个子问题,然后分别求解这两个子问题,直到收敛。
ALM 则是通过引入拉格朗日乘子,将约束优化问题转化为无约束优化问题,在核范数优化中,ALM 可以通过迭代更新拉格朗日乘子和矩阵 \(X\),逐步逼近最优解。
SVT 是一种专门针对核范数优化的算法,它基于奇异值分解(SVD)的思想,通过对矩阵的奇异值进行阈值处理,来实现核范数的最小化。
(二)面临的挑战
尽管核范数优化在理论和应用方面取得了显著的进展,但仍然面临一些挑战,对于大规模数据的核范数优化问题,现有的算法在计算效率和存储需求方面还存在一定的局限性,在处理高维图像或大规模数据集时,传统的算法可能需要消耗大量的计算时间和内存资源。
核范数优化问题的求解往往依赖于矩阵的奇异值分解,而奇异值分解的计算复杂度较高,尤其是在处理大规模矩阵时,如何降低奇异值分解的计算复杂度,提高核范数优化算法的效率,是一个重要的研究方向。
核范数优化问题的解可能不唯一,尤其是在存在多个满足约束条件的矩阵时,如何选择合适的解,以及如何保证解的稳定性和鲁棒性,也是需要进一步研究的问题。
四、核范数优化的未来发展趋势
随着人工智能、大数据和云计算等技术的不断发展,核范数优化将迎来更广阔的发展空间,研究人员将不断探索新的算法和理论,以提高核范数优化的效率和性能,结合深度学习和核范数优化的方法,可能会在图像处理、自然语言处理等领域取得更好的效果。
核范数优化将与其他领域的技术进行深度融合,形成更多的创新应用,在物联网中,可以利用核范数优化对传感器数据进行压缩和处理,实现能源高效的数据传输和分析;在医疗影像领域,核范数优化可以用于疾病诊断、图像分割和配准等方面,提高医疗影像的质量和准确性。
核范数优化作为一种重要的数学优化方法,具有广泛的应用前景和发展潜力,虽然目前还面临一些挑战,但随着技术的不断进步和研究的深入,相信核范数优化将在更多领域发挥重要作用,为解决复杂问题提供有力的支持,如果您对核范数优化有更深入的需求,上首页 SEO 网在这方面有一定的业务经验,可以为您提供专业的服务和解决方案,帮助您在相关领域取得更好的成果。
标签: 核范数


